Tutorial¶
Simple Example¶
The example below shows how easy it is to define a model that we could fit to.
from symfit import Parameter, Variable
a = Parameter('a')
b = Parameter('b')
x = Variable('x')
model = a * x + b
Lets fit this model to some generated data.
from symfit import Fit
import numpy as np
xdata = np.linspace(0, 100, 100) # From 0 to 100 in 100 steps
a_vec = np.random.normal(15.0, scale=2.0, size=(100,))
b_vec = np.random.normal(100.0, scale=2.0, size=(100,))
ydata = a_vec * xdata + b_vec # Point scattered around the line 5 * x + 105
fit = Fit(model, xdata, ydata)
fit_result = fit.execute()
Printing fit_result will give a full report on the values for every
parameter, including the uncertainty, and quality of the fit.
Initial Guess¶
For fitting to work as desired you should always give a good initial guess for
a parameter. The Parameter object can therefore
be initiated with the following keywords:
valuethe initial guess value. Defaults to1.minMinimal value for the parameter.maxMaximal value for the parameter.fixedWhether the parameter’svaluecan vary during fitting.
In the example above, we might change our
Parameter’s to the following after looking at a
plot of the data:
k = Parameter('k', value=4, min=3, max=6)
a, b = parameters('a, b')
a.value = 60
a.fixed = True
Accessing the Results¶
A call to Fit.execute returns a
FitResults instance. This object holds all information
about the fit. The fitting process does not modify the
Parameter objects. In the above example,
a.value will still be 60 and not the value we obtain after fitting. To
get the value of fit parameters we can do:
>>> print(fit_result.value(a))
>>> 14.66946...
>>> print(fit_result.stdev(a))
>>> 0.3367571...
>>> print(fit_result.value(b))
>>> 104.6558...
>>> print(fit_result.stdev(b))
>>> 19.49172...
>>> print(fit_result.r_squared)
>>> 0.950890866472
For more FitResults, see the Module Documentation.
Evaluating the Model¶
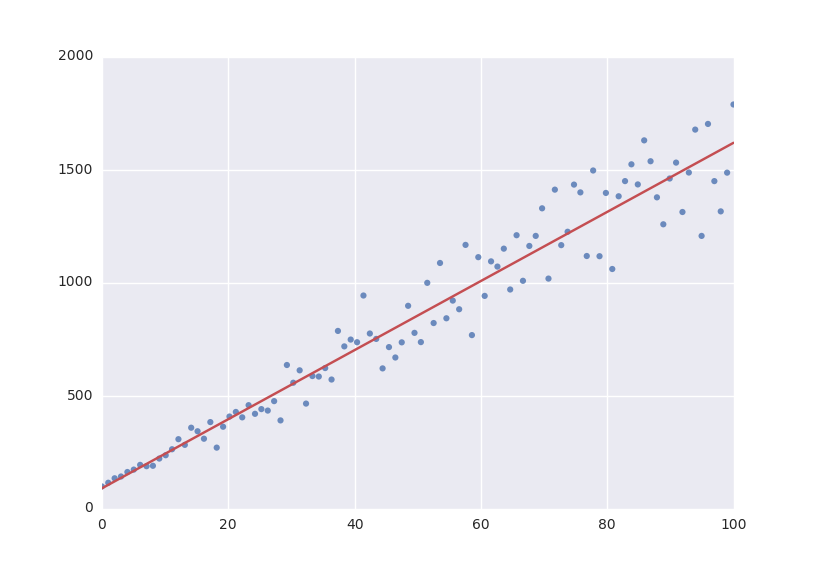
With these parameters, we could now evaluate the model with these parameters so we can make a plot of it. In order to do this, we simply call the model with these values:
import matplotlib.pyplot as plt
y = model(x=xdata, a=fit_result.value(a), b=fit_result.value(b))
plt.plot(xdata, y)
plt.show()
The model has to be called by keyword arguments to prevent any ambiguity. So the following does not work:
y = model(xdata, fit_result.value(a), fit_result.value(b))
To make life easier, there is a nice shorthand notation to immediately use a fit result:
y = model(x=xdata, **fit_result.params)
This immediately unpacks an OrderedDict containing the optimized fit
parameters.
Named Models¶
More complicated models are also relatively easy to deal with by using named models. Let’s try our luck with a bivariate normal distribution:
from symfit import parameters, variables, exp, pi, sqrt
x, y, p = variables('x, y, p')
mu_x, mu_y, sig_x, sig_y, rho = parameters('mu_x, mu_y, sig_x, sig_y, rho')
z = (
(x - mu_x)**2/sig_x**2
+ (y - mu_y)**2/sig_y**2
- 2 * rho * (x - mu_x) * (y - mu_y)/(sig_x * sig_y)
)
model = {
p: exp(
- z / (2 * (1 - rho**2)))
/ (2 * pi * sig_x * sig_y * sqrt(1 - rho**2)
)
}
fit = Fit(model, x=xdata, y=ydata, p=pdata)
By using the magic of named models, the flow of information is still relatively clear, even with such a complicated function.
This syntax also supports vector valued functions:
model = {y_1: a * x**2, y_2: 2 * x * b}
One thing to note about such models is that now model(x=xdata) obviously no
longer works as type(model) == dict. There is a preferred way to resolve
this. If any kind of fitting object has been initiated, it will have a
.model atribute containing an instance of
Model. This can again be called:
a, b = parameters('a, b')
y_1, y_2, x = variables('y_1, y_2, x')
model = {y_1: a * x**2, y_2: 2 * x * b}
fit = Fit(model, x=xdata, y_1=y_data1, y_2=y_data2)
fit_result = fit.execute()
y_1_result, y_2_result = fit.model(x=xdata, **fit_result.params)
This returns a namedtuple(), with the components evaluated.
So through the magic of tuple unpacking, y_1 and y_2 contain the
evaluated fit. The dependent variables will be ordered alphabetically in the
returned namedtuple(). Alternatively, the unpacking can be
performed explicitly.
If for some reason no Fit is initiated you can make a
Model object yourself:
model = Model(model_dict)
y_1_result, y_2_result = model(x=xdata, a=2.4, b=0.1)
or equivalently:
outcome = model(x=xdata, a=2.4, b=0.1)
y_1_result = outcome.y_1
y_2_result = outcome.y_2